座標 変換 行列
二次元座標平面上においてxy を原点中心に反時計回りにθ回転させた点の座標 XY は回転行列を用いて計算することができます中心が原点でない回転も計算できます. Matrix cv.

三次元の座標の回転をexcelで計算したい 回転行列 三次元座標での Excel エクセル 教えて Goo
2次元座標変換行列

オイラー角と回転行列間の変換 オイラー角速度による回転行列変化
特に となる は回転だけでなく座標反転を含む 単位行列の行列式は なのでそこから に到達するには不連続な変換が必要になることから分かる の回転行列は純粋な回転のみからなり本義回転.

座標 変換 行列. SrcPt info. これまで立体の移動やポリゴンの頂点位置指定などにおいて 空間中の一点の位置を指定するのに x y z の3つの数値の組を使ってきました. 例えば先の座標系Aの中でq_Aが実は別の座標系B内の固定点Xをすでに移動して回転してA座標系で算出したものと考えれば left beginarrayc q_A 1 endarray right.
多重積分の座標変換で必要になる体積素の変換式ヤコビの定理を導くと以下の様になる ここで解りにくい所は上記の 1線形座標変換線形写像を行列表示できる 2行列の積を行列式の積に変換できる. 行列を用いて1次変換を表すときベクトルまたは点の座標は列ベクトルとして表しこれに対して正方行列を左から掛けるものとする ベクトル x y や点 Px y を と書く. は行列を C は変換を意味して C で変換行列とする上付きや下付きの文字は座標系を表すこれらを組み合わせた αβ C abc は a b c 軸座標系から α β 軸座標系への変換行列を表わすまた αβ i は電流を α β 軸座標系で表現した.
変換前後の座標からホモグラフィ行列を求める info. 基底変換するための変換行列を求めてみる 計算方法は簡単で行列の計算をするだけだ 高校の数学で習う行列の計算なのだ 注意 私の高校時代は行列を習ったのだが 2012年頃からの高校数学では行列が. ある座標系においてx yで表される位置pを各軸を原点を中心にθだけ回転しtだけ並行移動した座標系における表記x yに変換する場合以下のように計算できます まず元の座標系でpを表すと以下のようになります.
座標変換 2次元と3次元の座標変換 ロボット用なので回転と平行移動のみ 同次変換オイラー角 回転行列からオイラー角のパラメータ抽出を行う It_lives_vainlyの日記 剛体の運動には必ず回転軸があることの証明をば Rukeのページ. 概要 座標変換とは平行移動や回転などを駆使して求めたい座標に変換することで 3d座標のオブジェクトを2d座標に変換し最終的にスクリーンウィンドウに 描画するために使われています3dに関する座標の用語が出るのでワールド座標やビュー座標という単語に 聞き覚え. 行列 xy および z の対応する要素で定義された 3 次元の直交座標を球面座標 azel および r に変換します これらの点は立方体の 8 つの頂点に対応します.
GetPerspectiveTransform info. そしてこの変換は同次座標系で表された変換でした同次座標系を使わない場合の変換はこちらになります ちょっとこのままでは使いにくいので回転行列をR並進ベクトルをtとおきます この同次座標を使わない形を覚えておいてください. Rect 1 0 10j print cmath.
Rect 1 1 0540302305868139808414709848078965j print cmath. Polar c 1 1. Polar c 0 cmath.
Rect cmath. 逆方向回転変換は回転方向が逆とみなして θ に θ を代入して得られる回転座標変換のポイントは座標軸の回転の順と逆を見分けることにある例の回転は x 軸から y 軸に向かう反時計回りでありこの方向が順回転である. 極座標から直交座標への変換はcmathrectを使う cmathrect絶対値 偏角 のように引数を指定すると等価な複素数 complex 型の値が取得できる print cmath.
このページではアフィン変換についての解説とアフィン変換を用いたC言語の画像処理プログラムの紹介をします スポンサーリンク Contentsアフィン変換とはアフィン変換とは線形変換平行移動線形変換とは平行移動とはア. OpenGLには投影変換行列を設定してくれる関数がありますglFrustum関数は前方クリッピング面の左右上下の座標 lrtb とZ軸の距離 n および遠方クリッピング面のZ軸の距離 f を指定して透視投影変換行列を設定しますgluPerspective関数は視野角fovyとアスペクト比aspect前方後方.
図解でわかる Arkitのtransform理解のための4 4行列の説明 Qiita

行列で座標変換をする Gutugutu3030
座標回転公式と球面三角法

回転行列の表式と導出 2次元 3次元 Notes Jp
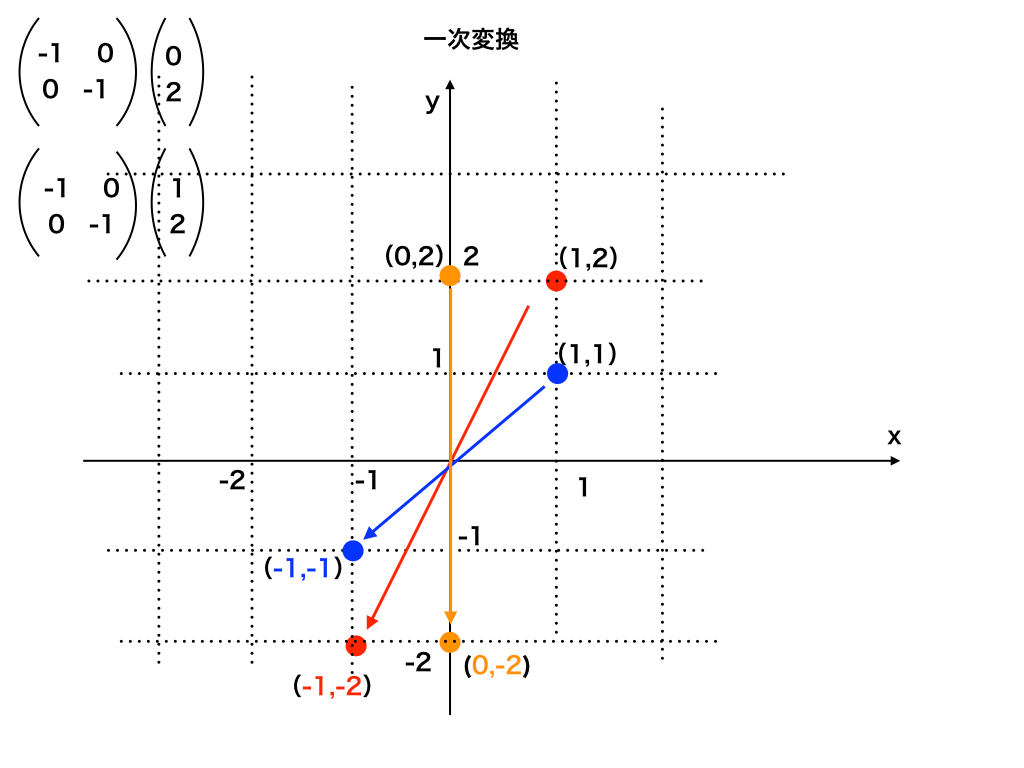
一次変換って何 イラストで理解するわかりやすい線形代数入門4
姿勢変換行列 Thoth Children
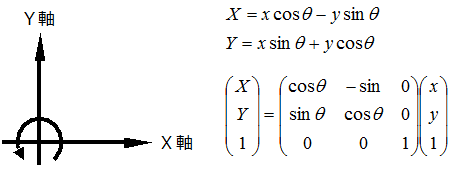
回転行列 拡大縮小行列 平行移動行列 三次元座標の場合 イメージングソリューション
座標回転公式と球面三角法